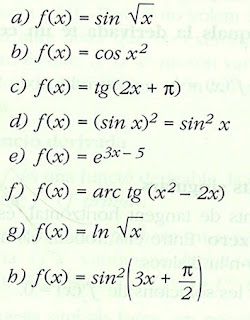viernes, 13 de noviembre de 2015
CLASSE Nº9: LLENGUATGE MATEMÀTIC
9.- COM ANOMENEM LES FUNCIONS I LES DERIVADES
Funcions i variables
Per a anomenar una funció, utilitzem una lletra. Per exemple f, g, h,... Una funció lliga dues variables. Per exemple, x i z. Posem z=f(x).
Paràmetres
Per a designar el valor que pren una funció f per a un cert valor de x, per exemple, 4, posem f(4). Però si no volem concretar aquest valor de x, aleshores posem a o c o una altra lletra que no exercisca, habitualment, el paper de "variable": f(a), f(c),... Però és que a o c no són variables? Sí, ho són perquè varien, és a dir, poden pendre valors variats. Peò no són la variable de la funció. Anomenem aquestes lletres paràmetres.
Funció derivada
Si f és una funció derivable, la derivada és, obviament, una altra funció. Saps que es designa f' (f prima).
Prima significa primera (mira-ho al diccionari). La funció derivada de f', que es designaria (f')' s'anommena derivada segona de f i es denota simplement així: f'' (f segona). Anàlogament, (f'')'=f''' (derivada de f'' és d tercera).
Posem f'o Df?
f' és el nom d'una funció nova. Df és l'ordre de derivar la funció f i el resultat és f', és a dir, Df=f'. Segons això, podem posar D(x+1-cos x), però no es correcte posar (x+1-cos x)' encara que de vegades s'escriu i no és massa greu.
CLASSE Nº8: REPRESENTACIÓ DE FUNCIONS RACIONALS
8.- REPRESENTACIÓ DE FUNCIONS RACIONALS
Les funcions racional són se la forma P(x)/Q(x), on P(x) i Q(x) són plinomis. Per exemple:
Aquelles que tractarem ací són d'un nivell similar a les anteriors, amb denominadors de grau un o dos. Totes tenen la curiosa peculiaritat que coneixent perfectament totes les branques infinites, podrem fer un esbós molt aproximat de la corba.
Per representar una funció racional simplificada P(x)/Q(x). trobarem:
1.- Asímptotes verticals.Les arrels del denominador (solucions de léquació Q(x)=0 són les abscisses de las asímptotes verticals. Les obtenim juntamente amb la posició de la corba respecte de elles.
2.- Asímptotes horitzontals i obliqües
- Si grau de P(x) < grau de Q(x), hi ha asímptota horitzontal.
- Si grau de P(x)= grau de Q(x)+1, hi ha asímptota obliqua.
Si n'hi ha, trobem l'asímptota horitzontal o obliqua i la posició respecte d'ella.
- Si grau de P(x)-grau de Q(x) >12, no hi ha asímptota horitzontal ni obliqua, però sí branques infinites en +-infinito.
Amb totes aquestes branques infinites quasi sempre podem fer un esbós molt aproximat a la forma de la corba.
3.- Punta singulars. Les abscises són les solucions f'(x)=0.
4.- Altres punts. Els podem obtindre si volem més precisió.
8.2.- EXERCICIS RESOLTS
EXERCICI 1: Representa la següent funció de la qual coneixem les asímptotes i la posició de la corba respecte a aquesta:

EXERCICI 2: Representa la següent funció de la qual sabem que no té asímptotes verticals i coneixem l'asímptota obliqua:

EXERCICI 3: Representa la següent funció de la qual coneixem les asímptotes verticals, l'horitzontal i la posició de la corba respecte d'aquestes:


8.3.- EXERCICIS PROPOSATS
EXERCICI 1:
CLASSE Nº7: REPRESENTACIÓ DE FUNCIONS POLINÒMIQUES
7.- REPRESENTACIÓ DE FUNCIONS POLINÒMIQUES
Les funcions polinòmiques són de la forma P(x), on P(x) és un polinomi. Per exemple:Són funcions contínues, amb només dues branques infinites (en -infinito i en + infinito).
Si a més de coneixer les branques infinites localitzem tots els punt de tangent horitzontal (punts singulars), podrem representar-les amb molta precisió.
Per representar una funció polinòmica, P(x), de grau major que dos:
- Trobem dues branques infinites:
- Resolem l'equació P'(x)=0. Les solucions, si n'hi ha, són les abscisses dels punts singulars. A continuació, se n'obtenen les ordenades.
- S'unixen els punts obtinguts entre si i amb les branques infinites, anant a espai de no dibuixar altres punts singulars que els ja obtinguts. d'aquesta manera, esbrinem quins són els màxims i mínims relatius.
- Si podem, convé obtindre, també, els punts de tall amb els eixos per a aconseguir una major precisió en la representació.
7.1.- EXERCICIS RESOLTS
EXERCICI 1: Representa la funció polinòmica següent:EXERCICI 2: Representa la funció polinòmica següent:
7.2.- EXERCICIS PROPOSATS
EXERCICI 1:CLASSE Nº6: UTILITAT DE LA FUNCIÓ DERIVADA
6.- UTILITAT DE LA FUNCIÓ DERIVADA
Quan una funció ens ve donada per l'expressió analítica, f(x), derivada, f'(x), ens dóna la inclinació (el pendent) de la corba a cada punt. Vegem-ne, en concret, algunes de les aplicacions.
Càlcul de la derivada d'una funció en diversos punts.
Per trobar f'(a), f'(b), f'(c),..., es procedix així:
- S'obté l'expressió general de f'(x).
- Es substituïx en f'(x) la x per a, b, c,...
Obtenció de les abscisses en les quals la derivada té un cert valor.
Per esbrinar els valors de x tals que f'(x)=k, es procedix així:
- S'obté l'expressió general de f'(x).- Es resol l'equació de f'(x)=k.
Obtenció de les abscisses dels punts singulars.
Anomenem punts singulars els punts de tangent horitzontal, és a dir, els punts en què la derivada és zero. Entre ells trobem els màxims i mínims relatius, però por haver-n'hi d'altres.
Les abscisses dels punts singulars són les solucions de f'(x)=0.
Obtenció de trams on la corba creix o decreix.
Si f'(x)>0, la funció és creixent, i si f'(x)>0, la corba és decreixent. Per tant, resolent aquestes inequacions s'obtenen els intervals on la corba creix o decreix.
6.2.- EXERCICIS RESOLTS
Donada la funció següent:
a) Troba la derivada de la funció en els punts -1, 0, 2 i 4.
b) Troba la recta tangent en el punt d'ascissa x=2.
c) Esbrina les abscisses dels possibles màxims i mínims relatius.
d) En x=4, és creixent o decreixent?
6.3.- EXERCICIS PROPOSATS
EXERCICI 1: Calcula la funció derivada de la funció següent:
a) Els pendents de les rectes tangents a les abscisses -1, 1 i 3.
b) Les equacions d'aquestes rectes tangents.
c) Les abscisses dels possibles màxims i mínims relatius.
d) És f(x) creixent o decreixent en x=2?
CLASSE nº5: DERIVADA D'UNA FUNCIÓ COMPOSTA. REGLA DE LA CADENA
CLASSE Nº2: CREIXIMENT D'UNA FUNCIÓ EN UN PUNT. DERIVADA
2.- CREIXIMENT D’UNA FUNCIÓ EN UN PUNT. DERIVADA
 El creiximent d'una funció en un punt ve donat, de forma natural, pel creixement (el pendent) de la recta tangent a la corba en aquest punt.
El creiximent d'una funció en un punt ve donat, de forma natural, pel creixement (el pendent) de la recta tangent a la corba en aquest punt.Així, la mesura del creixement de la funció adjunta en els punts A, B, c i d és, respectivamente 2, -1, 0 i 2'5 (comprova-ho).
En aquest apartat aprendrem a calcular el creixement en un punt de funcions donades no ja gràficament, sinó mitjançcant les seues expressions analítiques.
2.1.- RELACIÓN DEL CREIXEMENT EN UN PUNT AMB LA TVM
La TVM d'una funció en un interval s'interpreta com el pendent de la corda corresponents. Segons això, serà:
TVM [a, b1] = pendent de AB1.
TVM [a, b2] = pendent de AB2.
TVM [a, b3] = pendent de AB3.
La recta tangent t s'obté com a límit de les secants AB1, AB2, AB3, ... Per tant, el pendent és el límit dels pendents de les secants, ABi quan Bi s'apropa a A.
2.2.- DERIVADA D'UNA FUNCIÓ EN UN PUNT
El creixement d'una funció en un punt es mesura del pendent tangent al gràfic de la funció en aquest punt. s'obté mitjanç l'expressió següent:Aquest valor el anomenem derivada de f en a, es designa per f'(a).
2.3.- EXERCICIS RESOLTS
EXERCICI 1: Troba el valor de la derivada de la següent funció en els punts x=1, x=0 i x=3.EXERCICI 2: Troba la derivada de la funció f(x) = 3/(x-2) en x=4.
2.4.- EXERCICIS PROPOSATS
EXERCICI 1: Troba la derivada de la següent funció en els punts d'abscisses 4 i 5.EXERCICI 2: Troba la derivada de la funció f(x) = 3/(x-2) en els punts d'abscisses 1, -1 i 5.
EXERCICI 3: Troba la derivada de la funció f(x) = 1/x en els punts d'abscisses -2, -1, 1 i 2.
CLASSE Nº4: REGLES PER A OBTINDRE LES DERIVADES D'ALGUNES FUNCIONS
4.- REGLES PER A OBTINDRE LES DERIVADES D'ALGUNES FUNCIONS
A la classe anterior hem calculat la derivada d'algunes funcións aplicant la definició de derivada. El procés és llarg i pesat. No obstant això, hi a unes senzilles regles pràctiques amb les quals podem trobar, molt fàcilment, la derivada de qualsevol funció elemental.
4.1.- Derivada d'una funció constant.
4.2.- Derivada de x

4.3.- Derivada d'una funció potència
4.4.- Derivada del producte d'un nombre per una funció
4.5.- Derivada de la suma de funcions
4.6.- Derivada de les funcions trigonomètriques
4.7.- Derivada de les funcions arc
4.8.- Derivada de les funcions exponencials
4.9.- Derivada de les funcions logarítmiques
4.10.- Derivada del producte de dues funcions
4.11.- Derivada del quocient de dues funcions
4.12.- EXERCICIS PROPOSATS
Suscribirse a:
Comentarios (Atom)